Confidence interval
In statistics, a confidence interval (CI) is a particular kind of interval estimate of a population parameter. Instead of estimating the parameter by a single value, an interval likely to include the parameter is given. Thus, confidence intervals are used to indicate the reliability of an estimate. How likely the interval is to contain the parameter is determined by the confidence level or confidence coefficient. Increasing the desired confidence level will widen the confidence interval.
A confidence interval is always qualified by a particular confidence level, usually expressed as a percentage; thus one speaks of a "95% confidence interval". The end points of the confidence interval are referred to as confidence limits.
The calculation of a confidence interval generally requires assumptions about the nature of the estimation process – it is primarily a parametric method – for example, it may depend on an assumption that the distribution of the population from which the sample came is normal. As such, confidence intervals as discussed below are not robust statistics, though modifications can be made to add robustness – see robust confidence intervals.
Confidence intervals are used within Neyman–Pearson (frequentist) statistics; in Bayesian statistics a similar role is played by the credible interval, but the credible interval and confidence interval have different conceptual foundations and in general they take different values. As part of the general debate between frequentism and Bayesian statistics, there is disagreement about which of these statistics is more useful and appropriate, as discussed in alternatives and critiques.
Contents |
Conceptual basis

Interval estimates can be contrasted with point estimates. A point estimate is a single value given as the estimate of a population parameter that is of interest, for example the mean of some quantity. An interval estimate specifies instead a range within which the parameter is estimated to lie. Confidence intervals are commonly reported in tables or graphs along with point estimates of the same parameters, to show the reliability of the estimates.
For example, a confidence interval can be used to describe how reliable survey results are. In a poll of election voting-intentions, the result might be that 40% of respondents intend to vote for a certain party. A 90% confidence interval for the proportion in the whole population having the same intention on the survey date might be 38% to 42%. From the same data one may calculate a 95% confidence interval, which might in this case be 36% to 44%. A major factor determining the length of a confidence interval is the size of the sample used in the estimation procedure, for example the number of people taking part in a survey.
Confidence intervals are closely related to statistical significance testing. In many situations, if the point estimate of a parameter is X, with confidence interval [a,b] at confidence level P, then any value outside the interval [a,b] will be significantly different from X at significance level α = 1 − P, under the same distributional assumptions that were made to generate the confidence interval. That is to say, if in an estimation of a second parameter we observed a value less than a or greater than b, we would reject the null hypothesis that the true value of this parameter equaled X, at the α level of significance; and conversely, if the estimate of the second parameter lay within the interval [a,b], we would be unable to reject the null hypothesis that the parameter equaled X. In consequence, if the estimates of two parameters (for example, the mean values of a variable in two independent groups of objects) have confidence intervals at a given P value that do not overlap, it is very likely that the two values are significantly different at the corresponding value of α. However, this is not exactly true since the test of the significance of the difference between the two means will depend on the sampling distribution of that difference, whereas the confidence intervals are related to the sampling distribution of the two absolute values.[1][2]
Confidence regions generalize the confidence interval concept to deal with multiple quantities. Such regions can indicate not only the extent of likely estimation errors but can also reveal whether (for example) it is the case that if the estimate for one quantity is unreliable then the other is also likely to be unreliable. See also confidence bands.
In applied practice, confidence intervals are typically stated at the 95% confidence level.[3] However, when presented graphically, confidence intervals can be shown at several confidence levels, for example 50%, 95% and 99%.
Statistical theory
Definition
Confidence intervals as random intervals
Confidence intervals are constructed on the basis of a given dataset: x denotes the set of observations in the dataset, and X is used when considering the outcomes that might have been observed from the same population, where X is treated as a random variable whose observed outcome is X = x. A confidence interval is specified by a pair of functions u(.) and v(.) and the confidence interval for the given data set is defined as the interval (u(x), v(x)). To complete the definition of a confidence interval, there needs to be a clear understanding of the quantity for which the CI provides an interval estimate. Suppose this quantity is w. The property of the rules u(.) and v(.) that makes the interval (u(x), v(x)) closest to what a confidence interval for w would be, relates to the properties of the set of random intervals given by (u(X), v(X)): that is treating the end-points as random variables. This property is the coverage probability or the probability c that the random interval includes w.
Here the endpoints U = u(X) and V = v(X) are statistics (i.e., observable random variables) which are derived from values in the dataset. The random interval is (U, V).
Confidence intervals for inference
For the above to provide a viable means to statistical inference, something further is required: a tie between the quantity being estimated and the probability distribution of the outcome X. Suppose that this probability distribution is characterised by the unobservable parameter θ, which is a quantity to be estimated, and by other unobservable parameters φ which are not of immediate interest. These other quantities φ in which there is no immediate interest are called nuisance parameters, as statistical theory still needs to find some way to deal with them.
The definition of a confidence interval for θ for any number α between 0 and 1 is an interval
for which
and u(X) and v(X) are observable random variables, i.e. one need not know the value of the unobservable quantities θ, φ in order to know the values of u(X) and v(X).
The number 1 − α (sometimes reported as a percentage 100%·(1 − α)) is the confidence level, sometimes called the confidence coefficient. Most standard books adopt this convention, where α will be a small number. Here Prθ,φ is used to indicate the probability when the random variable X has the distribution characterised by (θ, φ). An important part of this specification is that the random interval (U, V) covers the unknown value θ with a high probability no matter what the true value of θ actually is.
Note that here Prθ,φ need not refer to an explicitly given parameterised family of distributions, although it often does. Just as the random variable X notionally corresponds to other possible realisations of x from the same population or from the same version of reality, the parameters (θ, φ) indicate that we need to consider other versions of reality in which the distribution of X might have different characteristics.
Intervals for random outcomes
Confidence intervals can be defined for random quantities as well as for fixed quantities as in the above. See prediction interval. For this, consider an additional single-valued random variable Y which may or may not be statistically dependent on X. Then the rule for constructing the interval (u(x), v(x)) provides a confidence interval for the as-yet-to-be observed value y of Y if
Here Prθ,φ is used to indicate the probability over the joint distribution of the random variables (X, Y) when this is characterised by parameters (θ, φ).
Approximate confidence intervals
For non-standard applications it is sometimes not possible to find rules for constructing confidence intervals that have exactly the required properties. But practically useful intervals can still be found. The coverage probability c(θ, φ) for a random interval is defined by
and the rule for constructing the interval may be accepted as providing a confidence interval if
to an acceptable level of approximation.
Comparison to Bayesian interval estimates
A Bayesian interval estimate is called a credible interval. Using much of the same notation as above, the definition of a credible interval for the unknown true value of θ is, for a given α[4],
Here Θ is used to emphasize that the unknown value of θ is being treated as a random variable. The definitions of the two types of intervals may be compared as follows.
- The definition of a confidence interval involves probabilities calculated from the distribution of X for given (θ, φ) (or conditional on these values) and the condition needs to hold for all values of (θ, φ).
- The definition of a credible interval involves probabilities calculated from the distribution of Θ conditional on the observed values of X = x and marginalised (or averaged) over the values of Φ, where this last quantity is the random variable corresponding to the uncertainty about the nuisance parameters in φ.
Note that the treatment of the nuisance parameters above is often omitted from discussions comparing confidence and credible intervals but it is markedly different between the two cases.
In some simple standard cases, the intervals produced as confidence and credible intervals from the same data set can be identical. They are always very different if moderate or strong prior information is included in the Bayesian analysis.
Desirable properties
When applying standard statistical procedures, there will often be standard ways of constructing confidence intervals. These will have been devised so as to meet certain desirable properties, which will hold given that the assumptions on which the procedure rely are true. These desirable properties may be described as: validity, optimality and invariance. Of these "validity" is most important, followed closely by "optimality". "Invariance" may be considered as a property of the method of derivation of a confidence interval rather than of the rule for constructing the interval. In non-standard applications, the same desirable properties would be sought.
- Validity. This means that the nominal coverage probability (confidence level) of the confidence interval should hold, either exactly or to a good approximation.
- Optimality. This means that the rule for constructing the confidence interval should make as much use of the information in the data-set as possible. Recall that one could throw away half of a dataset and still be able to derive a valid confidence interval. One way of assessing optimality is by the length of the interval, so that a rule for constructing a confidence interval is judged better than another if it leads to intervals whose lengths are typically shorter.
- Invariance. In many applications the quantity being estimated might not be tightly defined as such. For example, a survey might result in an estimate of the median income in a population, but it might equally be considered as providing an estimate of the logarithm of the median income, given that this is a common scale for presenting graphical results. It would be desirable that the method used for constructing a confidence interval for the median income would give equivalent results when applied to constructing a confidence interval for the logarithm of the median income: specifically the values at the ends of the latter interval would be the logarithms of the values at the ends of former interval.
Methods of derivation
For non-standard applications, there are several routes that might be taken to derive a rule for the construction of confidence intervals. Established rules for standard procedures might be justified or explained via several of these routes. Typically a rule for constructing confidence intervals is closely tied to a particular way of finding a point estimate of the quantity being considered.
- Statistics
- This is closely related to the method of moments for estimation. A simple example arises where the quantity to be estimated is the mean, in which case a natural estimate is the sample mean. The usual arguments indicate that the sample variance can be used to estimate the variance of the sample mean. A naive confidence interval for the true mean can be constructed centered on the sample mean with a width which is a multiple of the square root of the sample variance.
- Likelihood theory
- Where estimates are constructed using the maximum likelihood principle, the theory for this provides two ways of constructing confidence intervals or confidence regions for the estimates.
- Estimating equations
- The estimation approach here can be considered as both a generalization of the method of moments and a generalization of the maximum likelihood approach. There are corresponding generalizations of the results of maximum likelihood theory that allow confidence intervals to be constructed based on estimates derived from estimating equations.
- Via significance testing
- If significance tests are available for general values of a parameter, then confidence intervals/regions can be constructed by including in the 100p% confidence region all those points for which the significance test of the null hypothesis that the true value is the given value is not rejected at a significance level of (1-p).
Examples
Practical example

A machine fills cups with margarine, and is supposed to be adjusted so that the content of the cups is 250 g of margarine. As the machine cannot fill every cup with exactly 250 g, the content added to individual cups shows some variation, and is considered a random variable X. This variation is assumed to be normally distributed around the desired average of 250 g, with a standard deviation of 2.5 g. To determine if the machine is adequately calibrated, a sample of n = 25 cups of margarine is chosen at random and the cups are weighed. The resulting measured masses of margarine are X1, ..., X25, a random sample from X.
To get an impression of the expectation μ, it is sufficient to give an estimate. The appropriate estimator is the sample mean:
The sample shows actual weights x1, ..., x25, with mean:
If we take another sample of 25 cups, we could easily expect to find mass values like 250.4 or 251.1 grams. A sample mean value of 280 grams however would be extremely rare if the mean content of the cups is in fact close to 250 grams. There is a whole interval around the observed value 250.2 grams of the sample mean within which, if the whole population mean actually takes a value in this range, the observed data would not be considered particularly unusual. Such an interval is called a confidence interval for the parameter μ. How do we calculate such an interval? The endpoints of the interval have to be calculated from the sample, so they are statistics, functions of the sample X1, ..., X25 and hence random variables themselves.
In our case we may determine the endpoints by considering that the sample mean X from a normally distributed sample is also normally distributed, with the same expectation μ, but with standard error σ/√n = 0.5 (grams). By standardizing, we get a random variable
dependent on the parameter μ to be estimated, but with a standard normal distribution independent of the parameter μ. Hence it is possible to find numbers −z and z, independent of μ, where Z lies in between with probability 1 − α, a measure of how confident we want to be. We take 1 − α = 0.95. So we have:
The number z follows from the cumulative distribution function:
and we get:
This might be interpreted as: with probability 0.95 we will find a confidence interval in which we will meet the parameter μ between the stochastic endpoints
and
This does not mean that there is 0.95 probability of meeting the parameter μ in the calculated interval. Every time the measurements are repeated, there will be another value for the mean X of the sample. In 95% of the cases μ will be between the endpoints calculated from this mean, but in 5% of the cases it will not be. The actual confidence interval is calculated by entering the measured masses in the formula. Our 0.95 confidence interval becomes:

As the desired value 250 of μ is within the resulted confidence interval, there is no reason to believe the machine is wrongly calibrated.
The calculated interval has fixed endpoints, where μ might be in between (or not). Thus this event has probability either 0 or 1. One cannot say: "with probability (1 − α) the parameter μ lies in the confidence interval." One only knows that by repetition in 100(1 − α) % of the cases, μ will be in the calculated interval. In 100α % of the cases however it does not. And unfortunately one does not know in which of the cases this happens. That is why one can say: "with confidence level 100(1 − α) %, μ lies in the confidence interval."
The figure on the right shows 50 realisations of a confidence interval for a given population mean μ. If we randomly choose one realisation, the probability is 95% we end up having chosen an interval that contains the parameter; however we may be unlucky and have picked the wrong one. We will never know; we are stuck with our interval.
Theoretical example
Suppose X1, ..., Xn are an independent sample from a normally distributed population with (parameters) mean μ and variance σ2. Let
be the well known statistics, sample mean and sample variance.
Then
has a Student's t-distribution with n − 1 degrees of freedom. Note that the distribution of T does not depend on the values of the unobservable parameters μ and σ2; i.e., it is a pivotal quantity. Suppose we wanted to calculate a 90% confidence interval for μ. Then, denoting c as the 95th percentile of this distribution,
(Note: "95th" and "0.9" are correct in the preceding expressions. There is a 5% chance that T will be less than −c and a 5% chance that it will be larger than +c. Thus, the probability that T will be between −c and +c is 90%.)
Consequently
and we have a theoretical (stochastic) 90% confidence interval for μ.
After observing the sample we find values x for X and s for S, from which we compute the confidence interval
an interval with fixed numbers as endpoints, of which we can no more say there is a certain probability it contains the parameter μ. Either μ is in this interval or isn't.
Relation to hypothesis testing
While the formulations of the notions of confidence intervals and of statistical hypothesis testing are distinct they are in some senses related and to some extent complementary. While not all confidence intervals are constructed in this way, one general purpose approach to constructing confidence intervals is to define a 100(1−α)% confidence interval to consist of all those values θ0 for which a test of the hypothesis θ=θ0 is not rejected at a significance level of 100α%. Such an approach may not always be available since it presupposes the practical availability of an appropriate significance test. Naturally, any assumptions required for the significance test would carry over to the confidence intervals.
It may be convenient to make the general correspondence that parameter values within a confidence interval are equivalent to those values that would not be rejected by an hypothesis test, but this would be dangerous. In many instances the confidence intervals that are quoted are only approximately valid, perhaps derived from "plus or minus twice the standard error", and the implications of this for the supposedly corresponding hypothesis tests are usually unknown.
Meaning and interpretation
For users of frequentist methods, various interpretations of a confidence interval can be given.
- The confidence interval can be expressed in terms of samples (or repeated samples): "Were this procedure to be repeated on multiple samples, the calculated confidence interval (which would differ for each sample) would encompass the true population parameter 90% of the time." [5] Note that this need not be repeated sampling from the same population, just repeated sampling [6].
- The explanation of a confidence interval can amount to something like: "The confidence interval represents values for the population parameter for which the difference between the parameter and the observed estimate is not statistically significant at the 10% level"[7]. In fact, this relates to one particular way in which a confidence interval may be constructed.
- The probability associated with a confidence interval may also be considered from a pre-experiment point of view, in the same context in which arguments for the random allocation of treatments to study items are made. Here the experimenter sets out the way in which they intend to calculate a confidence interval and know, before they do the actual experiment, that the interval they will end up calculating has a certain chance of covering the true but unknown value.[8] This is very similar to the "repeated sample" interpretation above, except that it avoids relying on considering hypothetical repeats of a sampling procedure that may not be repeatable in any meaningful sense. See Neyman construction.
In each of the above, the following applies: If the true value of the parameter lies outside the 90% confidence interval once it has been calculated, then an event has occurred which had a probability of 10% (or less) of happening by chance.
Meaning of the term "confidence"
There is a difference in meaning between the common usage of the word "confidence" and its statistical usage, which is often confusing to the layman, and this is one of the critiques of confidence intervals, namely that in application by non-statisticians, the term "confidence" is misleading.
In common usage, a claim to 95% confidence in something is normally taken as indicating virtual certainty. In statistics, a claim to 95% confidence simply means that the researcher has seen something occur that only happens one time in 20 or less. If one were to roll two dice and get double six (which happens 1/36th of the time, or about 3%), few would claim this as proof that the dice were fixed, although statistically speaking one could have 97% confidence that they were. Similarly, the finding of a statistical link at 95% confidence is not proof, nor even very good evidence, that there is any real connection between the things linked.
When a study involves multiple statistical tests, some laymen assume that the confidence associated with individual tests is the confidence one should have in the results of the study itself. In fact, the results of all the statistical tests conducted during a study must be judged as a whole in determining what confidence one may place in the positive links it produces. For example, say a study is conducted which involves 40 statistical tests at 95% confidence, and which produces 3 positive results. Each test has a 5% chance of producing a false positive, so such a study will produce 3 false positives about two times in three. Thus the confidence one can have that any of the study's positive conclusions are correct is only about 32%, well below the 95% the researchers have set as their standard of acceptance.
Alternatives and critiques
Confidence intervals are one method of interval estimation, and the most widely used in frequentist statistics. An analogous concept in Bayesian statistics is credible intervals, while an alternative frequentist method is prediction interval, which, rather than estimating parameters, estimates the outcome of future samples.
There is disagreement about which of these methods produces the most useful results: the mathematics of the computations are rarely in question – confidence intervals being based on sampling distributions, credible intervals being based on Bayes' theorem – but the application of these methods, the utility and interpretation of the produced statistics, is debated.
Users of Bayesian methods, if they produced an interval estimate, would in contrast to confidence intervals, want to say "My degree of belief that the parameter is in fact in this interval is 90%,"[9] while users of prediction intervals would instead say "I predict that the next sample will fall in this interval 90% of the time."
Confidence intervals are an expression of probability and are subject to the normal laws of probability. If several statistics are presented with confidence intervals, each calculated separately on the assumption of independence, that assumption must be honoured or the calculations will be rendered invalid. For example, if the statistic with the narrowest interval were selected for attention, that interval would no longer be the true interval for that statistic. The act of selection changes the probability and in this case widens the interval.
This is particularly important when confidence intervals are generated in order to perform statistical tests. If multiple tests are done and those that return positive results are selected from amongst them, the intervals used to conduct the test will change, and in most situations the tests will be rendered invalid.
An approximate confidence interval for a population mean can be constructed for random variables that are not normally distributed in the population, relying on the central limit theorem, if the sample sizes and counts are big enough. The formulae are identical to the case above (where the sample mean is actually normally distributed about the population mean). The approximation will be quite good with only a few dozen observations in the sample if the probability distribution of the random variable is not too different from the normal distribution (e.g. its cumulative distribution function does not have any discontinuities and its skewness is moderate).
One type of sample mean is the mean of an indicator variable, which takes on the value 1 for true and the value 0 for false. The mean of such a variable is equal to the proportion that have the variable equal to one (both in the population and in any sample). This is a useful property of indicator variables, especially for hypothesis testing. To apply the central limit theorem, one must use a large enough sample. A rough rule of thumb is that one should see at least 5 cases in which the indicator is 1 and at least 5 in which it is 0. Confidence intervals constructed using the above formulae may include negative numbers or numbers greater than 1, but proportions obviously cannot be negative or exceed 1. Additionally, sample proportions can only take on a finite number of values, so the central limit theorem and the normal distribution are not the best tools for building a confidence interval. See "Binomial proportion confidence interval" for better methods which are specific to this case.
See also
- p-value
- Confidence region
- Error bar
- Prediction interval
- Tolerance interval
- Bootstrapping (statistics)
- Binomial proportion confidence interval
- Robust confidence intervals
- Chebyshev's inequality
- Interval finite element
Online calculators
Notes
- ↑ Goldstein, H., & Healey, M.J.R. (1995). "The graphical presentation of a collection of means." Journal of the Royal Statistical Society, 158, 175–77.
- ↑ Wolfe R, Hanley J (Jan 2002). "If we're so different, why do we keep overlapping? When 1 plus 1 doesn't make 2". CMAJ 166 (1): 65–6. PMID 11800251. PMC 99228. http://www.cmaj.ca/cgi/pmidlookup?view=long&pmid=11800251.
- ↑ Zar, J.H. (1984) Biostatistical Analysis. Prentice Hall International, New Jersey. pp 43–45
- ↑ Bernardo JE, Smith, Adrian (2000). Bayesian theory. New York: Wiley. pp. 259. ISBN 0-471-49464-X.
- ↑ Cox DR, Hinkley DV. (1974) Theoretical Statistics, Chapman & Hall, p49, 209
- ↑ Kendall, M.G. and Stuart, D.G. (1973) The Advanced Theory of Statistics. Vol 2: Inference and Relationship, Griffin, London. Section 20.4
- ↑ Cox DR, Hinkley DV. (1974) Theoretical Statistics, Chapman & Hall, p214, 225, 233
- ↑ Neyman, J. (1937) "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability", Philosophical Transactions of the Royal Society of London A, 236, 333–380.
- ↑ Cox DR, Hinkley DV. (1974) Theoretical Statistics, Chapman & Hall, p390
References
- Fisher, R.A. (1956) Statistical Methods and Scientific Inference. Oliver and Boyd, Edinburgh. (See p. 32.)
- Freund, J.E. (1962) Mathematical Statistics Prentice Hall, Englewood Cliffs, NJ. (See pp. 227–228.)
- Hacking, I. (1965) Logic of Statistical Inference. Cambridge University Press, Cambridge.
- Keeping, E.S. (1962) Introduction to Statistical Inference. D. Van Nostrand, Princeton, NJ.
- Kiefer, J. (1977) "Conditional Confidence Statements and Confidence Estimators (with discussion)" Journal of the American Statistical Association, 72, 789–827.
- Neyman, J. (1937) "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability" Philosophical Transactions of the Royal Society of London A, 236, 333–380. (Seminal work.)
- Robinson, G.K. (1975) "Some Counterexamples to the Theory of Confidence Intervals." Biometrika, 62, 155–161.
- Reiczigel J. (2003) Confidence intervals for the binomial parameter: some new considerations. Statistics in Medicine, 22, 611–621.
- Reiczigel J., Abonyi-Toth Z., & Singer J. (2008) An exact confidence set for two binomial proportions and exact unconditional confidence intervals for the difference and ratio of proportions. Computational Statistics & Data Analysis, 52, 5046–5053.
- Smithson, M. (2003) Confidence intervals. Quantitative Applications in the Social Sciences Series, No. 140. Belmont, CA: SAGE Publications. ISBN 9780761924999.
External links
- The Exploratory Software for Confidence Intervals tutorial programs that run under Excel
- Confidence interval calculators for R-Squares, Regression Coefficients, and Regression Intercepts
- Weisstein, Eric W., "Confidence Interval" from MathWorld.
- CAUSEweb.org Many resources for teaching statistics including Confidence Intervals.
- An interactive introduction to Confidence Intervals
- Confidence Intervals: Confidence Level, Sample Size, and Margin of Error by Eric Schulz, the Wolfram Demonstrations Project.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


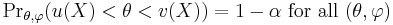


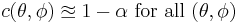





![\begin{align}
\Phi(z) & = P(Z \le z) = 1 - \tfrac{\alpha}2 = 0.975,\\[6pt]
z & = \Phi^{-1}(\Phi(z)) = \Phi^{-1}(0.975) = 1.96,
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d1a66e184d38aa014f61ac92990665df.png)
![\begin{align}
0.95 & = 1-\alpha=P(-z \le Z \le z)=P \left(-1.96 \le \frac {\bar X-\mu}{\sigma/\sqrt{n}} \le 1.96 \right) \\[6pt]
& = P \left( \bar X - 1.96 \frac{\sigma}{\sqrt{n}} \le \mu \le \bar X + 1.96 \frac{\sigma}{\sqrt{n}}\right) \\[6pt]
& = P\left(\bar X - 1.96 \times 0.5 \le \mu \le \bar X + 1.96 \times 0.5\right) \\[6pt]
& = P \left( \bar X - 0.98 \le \mu \le \bar X + 0.98 \right).
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b9555f77171a37a781c128ff35f4a5f0.png)








![\left[ \overline{x} - \frac{cs}{\sqrt{n}}, \overline{x} + \frac{cs}{\sqrt{n}} \right], \,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ea3c38f25868af0307c18f22302be974.png)